Decoding BPSK using Dot Product

2019-Mar-6

Based on the work of Phil Karn - KA9Q I have implemented a new BPSK Decoder for FoxTelem. After my talk at the AMSAT symposium, where I explained the Fox-1E BPSK endcoder and Costas loop decoderE, he pointed out that a Costas Loop is vulnerable to fading and loses track of the carrier. He suggested that a Dot Product decoder was a better approach. So I set out to see if that was true. Step 1 was understanding how a Dot Product BPSK decoder works and then implementing it in FoxTelem.

Dot Product Phase Change Detector

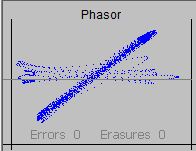A dot product is the product of two vectors. In this case we are going to be looking at the phase vector of the BPSK signal. In the phasor diagram to the right you see the phase vector plotted for many bits. This is a straight line because it is showing two phases that are 180 degrees apart, which sounds right for BPSK. In this case they are about 45 degrees and 225 degrees. It is a line rather than two dots because the amplitude is changing for each bit. This may well be an issue that needs to be addressed in the decoder.

Our signal is differentially encoded, making it DBPSK, and meaning that the absolute phase does not matter. We don't need it to oscillate between 0 and 180. Instead if the phase changes from one bit to the next then we have a "0", if the phase stays the same then we have a "1".

If we take the dot product of the phase from one bit and multiply it by the phase from the next bit, then we have a clear indication if the phase has changed. If the phase is the same then the dot product of two identical vectors is a vector with twice the length. If the phase is the opposite then the dot product should be zero. This is much less sensitive to phase inaccuracies than the Costas loop, which has to be locked to 0 and 180 degrees.

Are we aligned

We still need to be on the right frequency, even if we can tolerate some phase shift, and we still need to align with the data. That means we need to recover the carrier and the clock. The dot product calculation is very fast because it is not a convolution. So we simply run the calculation many times at different offsets and use the maximum magnitude (energy) to determine when we are aligned.

You can see the details in the FoxTelem code or look at Phil's original implementation in C. Broadly they both do the following:

1. Grab a buffer of audio data that holds 100 symbols at 48000 samples per second, or 40 samples per symbol for our 1200bps BPSK
2. Run a Dot product demodulation on every bit at every sample offset and a range of frequencies. Use this to determine the carrier frequency to +/-100Hz and the phase offset. Repeat this every few seconds but not every buffer
3. Run two dot product demodulations above and below the estimated carrier, one at +75Hz and one at -75Hz. We calculate the dot product of the symbols to approximately determine the bit sign and use it together with the cross product to work out if the frequency is positive or negative. Meaning our estimate was too high or two low. From the two results we estimate the carrier by linear interpolation
4. Finally we run the actual demodulation at the estimated carrier frequency and at a set of sample offset from early to late. Each sample offset is a phase offset. We use the magnitude to determine which offset was best and take those bits as the results. We use the calculated offset to adjust the phase for the next buffer.

In my next post I compare the performance of the Dot Product Decoder to the Costas Loop

73 Chris
g0kla/ac2Cz

Enter Comments Here:

Comments on this post